Field Ionization
Section author: Marco Garten
Module author: Marco Garten
Get started here https://github.com/ComputationalRadiationPhysics/picongpu/wiki/Ionization-in-PIConGPU
PIConGPU features an adaptable ionization framework for arbitrary and combinable ionization models.
Note
Most of the calculations and formulae in this section of the docs are done in the Atomic Units (AU) system.
AU |
SI |
|---|---|
length |
\(5.292 \cdot 10^{-11}\,\mathrm{m}\) |
time |
\(2.419 \cdot 10^{-17}\,\mathrm{s}\) |
energy |
\(4.360 \cdot 10^{-18}\,\mathrm{J}\quad\) (= 27.21 eV = 1 Rydberg) |
electrical field |
\(5.142 \cdot 10^{11}\,\frac{\mathrm{V}}{\mathrm{m}}\) |
Overview: Implemented Models
ionization regime |
implemented model |
reference |
|---|---|---|
Multiphoton |
None, yet |
|
Tunneling |
|
|
Barrier Suppression |
|
Attention
Models marked with “(R&D)” are under research and development and should be used with care.
Ionization Current
In order to conserve energy, PIConGPU supports an ionization current to decrease the electric field according to the amount of energy lost to field ioniztion processes. The current for a single ion is
It is assigned to the grid according to the macroparticle shape. \(E_\mathrm{ion}\) is the energy required to ionize the atom/ion, \(\mathbf{E}\) is the electric field at the particle position and \(V_\mathrm{cell}\) is the cell volume. This formula makes the assumption that the ejection energy of the electron is zero. See [Mulser]. The ionization current is accessible in speciesDefinition.param. To activate ionization current, set the second template of the ionization model to particles::ionization::current::EnergyConservation. By default the ionization current is deactivated.
Usage
Input for ionization models is defined in speciesDefinition.param, ionizer.param and ionizationEnergies.param.
Barrier Suppression Ionization
The so-called barrier-suppression ionization regime is reached for strong fields where the potential barrier binding an electron is completely suppressed.
Tunneling Ionization
Tunneling ionization describes the process during which an initially bound electron quantum-mechanically tunnels through a potential barrier of finite height.
Keldysh
The Keldysh ionization rate has been implemented according to the equation (9) in [BauerMulser1999]. See also [Keldysh] for the original work.
Note
Assumptions:
low field - perturbation theory
\(\omega_\mathrm{laser} \ll E_\mathrm{ip}\)
\(F \ll F_\mathrm{BSI}\)
tunneling is instantaneous
Ammosov-Delone-Krainov (ADK)
We implemented equation (7) from [DeloneKrainov] which is a simplified result assuming s-states (since we have no atomic structure implemented, yet).
Leaving out the pre-factor distinguishes ADKCircPol from ADKLinPol.
ADKLinPol results from replacing an instantaneous field strength \(F\) by \(F \cos(\omega t)\) and averaging over one laser period.
Attention
Be aware that \(Z\) denotes the residual ion charge and not the proton number of the nucleus! Be aware that \(e\) in \(D\) denotes Euler’s number, not the elementary charge
In the following comparison one can see the ADKLinPol ionization rates for the transition from Carbon II to III (meaning 1+ to 2+).
For a reference the rates for Hydrogen as well as the barrier suppression field strengths \(F_\mathrm{BSI}\) have been plotted.
They mark the transition from the tunneling to the barrier suppression regime.
(Source code, png, hires.png, pdf)
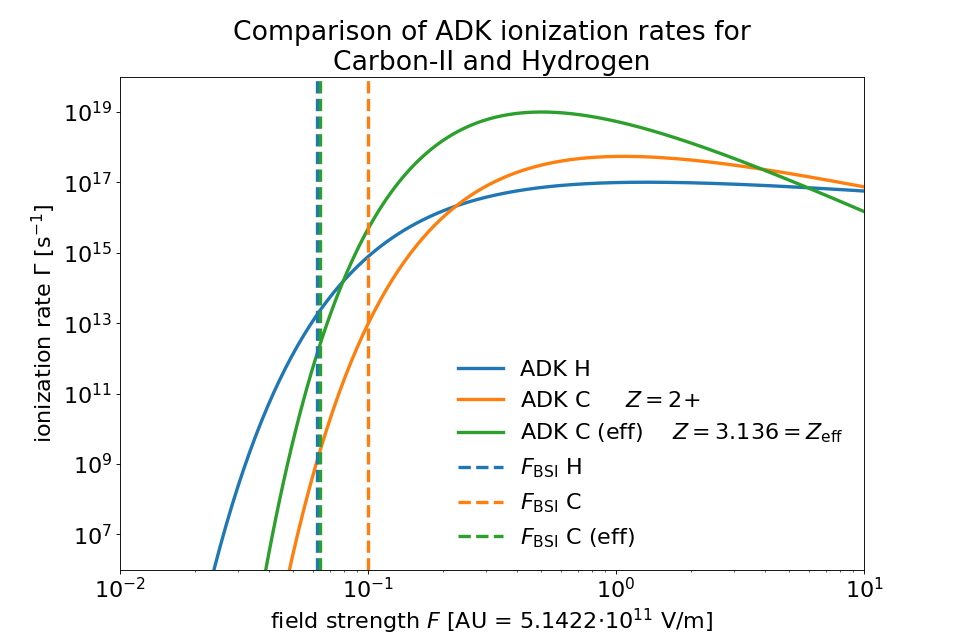
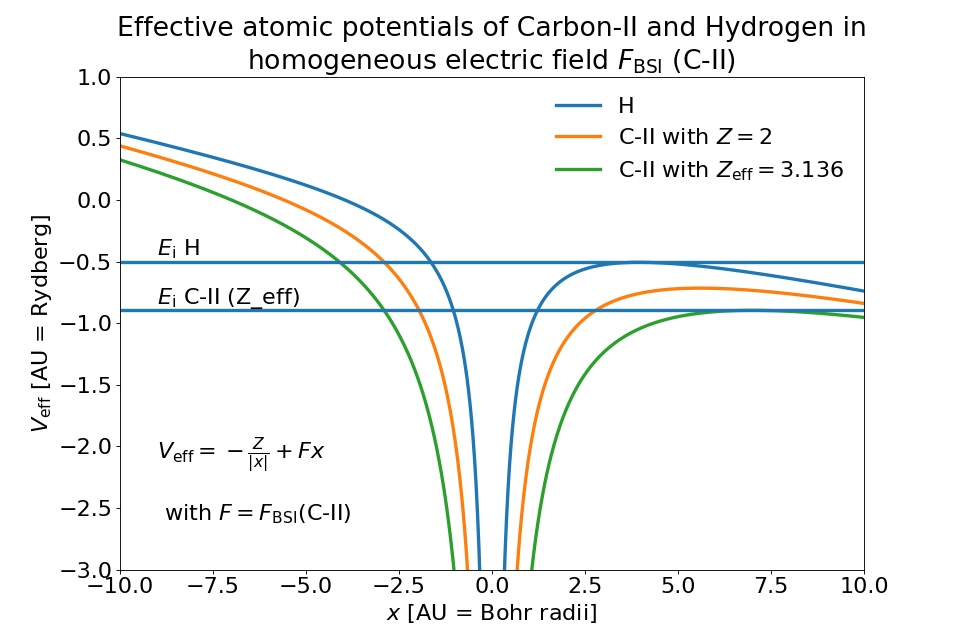
When we account for orbital structure in shielding of the ion charge \(Z\) according to [ClementiRaimondi1963] in BSIEffectiveZ the barrier suppression field strengths of Hydrogen and Carbon-II are very close to one another.
One would expect much earlier ionization of Hydrogen due to lower ionization energy. The following image shows how this can be explained by the shape of the ion potential that is assumed in this model.
(Source code, png, hires.png, pdf)
Predicting Charge State Distributions
Especially for underdense targets, it is possible to already give an estimate for how the laser pulse ionizes a specific target. Starting from an initially unionized state, calculating ionization rates for each charge state for a given electric field via a Markovian approach of transition matrices yields the charge state population for each time.
Here, we show an example of Neon gas ionized by a Gaussian laser pulse with maximum amplitude \(a_0 = 10\) and pulse duration (FWHM intensity) of \(30\,\mathrm{fs}\).
The figure shows the ionization rates and charge state population produced by the ADKLinPol model obtained from the pulse shape in the lower panel, as well as the step-like ionization produced by the BSI model.
You can test the implemented ionization models yourself with the corresponding module shipped in picongpu/lib/python.
import numpy as np
import scipy.constants as sc
from picongpu.utils import FieldIonization
# instantiate class object that contains functions for
# - ionization rates
# - critical field strengths (BSI models)
# - laser intensity conversion
FI = FieldIonization()
# dictionary with atomic units
AU = FI.atomic_unit
# residual charge state AFTER ionization
Z_H = 1
# hydrogen ionization energy (13.6 eV) converted to atomic units
E_H_AU = 13.6 * sc.electron_volt / AU['energy']
# output: 0.50
print("%.2f" % (E_H_AU))
# barrier suppression threshold field strength
F_BSI_H = FI.F_crit_BSI(Z=Z_H, E_Ip=E_H_AU)
# output: 3.21e+10 V/m
print("%.2e V/m" % (F_BSI_H * AU['electric field']))
References
N. B. Delone and V. P. Krainov. Tunneling and barrier-suppression ionization of atoms and ions in a laser radiation field, Phys. Usp. 41 469–485 (1998), http://dx.doi.org/10.1070/PU1998v041n05ABEH000393
D. Bauer and P. Mulser. Exact field ionization rates in the barrier-suppression regime from numerical time-dependent Schrödinger-equation calculations, Physical Review A 59, 569 (1999), https://dx.doi.org/10.1103/PhysRevA.59.569
P. Mulser and D. Bauer. High Power Laser-Matter Interaction, Springer-Verlag Berlin Heidelberg (2010), https://dx.doi.org/10.1007/978-3-540-46065-7
L.V. Keldysh. Ionization in the field of a strong electromagnetic wave, Soviet Physics JETP 20, 1307-1314 (1965), http://jetp.ac.ru/cgi-bin/dn/e_020_05_1307.pdf
E. Clementi and D. Raimondi. Atomic Screening Constant from SCF Functions, The Journal of Chemical Physics 38, 2686-2689 (1963) https://dx.doi.org/10.1063/1.1733573
E. Clementi and D. Raimondi. Atomic Screening Constant from SCF Functions. II. Atoms with 37 to 86 Electrons, The Journal of Chemical Physics 47, 1300-1307 (1967) https://dx.doi.org/10.1063/1.1712084
P. Mulser et al. Modeling field ionization in an energy conserving form and resulting nonstandard fluid dynamcis, Physics of Plasmas 5, 4466 (1998) https://doi.org/10.1063/1.873184