Collisional Ionization

Section author: Marco Garten, Brian Marre

PIConGPU features an adaptable ionization framework for arbitrary and combinable ionization models.

Note

This section describes the principal ideas and assumptions, limits and configuration options of implemented charge-state-only collisional ionization models.

Note

For a guide hot to setup a PIConGPU simulation with charge-state-only ionization see Ionization.

Local Thermal Equilibrium(LTE) models

Thomas-Fermi collisional Ionization

Module author: Marco Garten

PIConGPU implements the LTE Thomas-Fermi collisional ionization model according to [More1985], which uses the following input quantities

  • ion proton number \(Z\)

  • ion species mass density \(\rho\)

  • electron “temperature” \(T\)

to calculate the local mean ionization.

Limits of Thomas Fermi collisional ionization

The Thomas-Fermi ionization model is strictly valid only in equilibrium and in the semi-classical limit. Using it unmodified in the non-equilibirium situations typically encountered in PIC simulations may therefore lead to unphysical behaviour. To mitigate this partially, we have implemented several cutoffs to exclude regions where the model predictions are invalid.

To demonstrate the limits of the pure Thomas-Fermi ionization model, we will consider a compound plastic target, consisting of hydrogen(in blue) and carbon(in orange).

For this system we are plotting the average charge state for several electron temperatures over the ion mass density, the typical plastic density region is marked in green.

(Source code, png, hires.png, pdf)

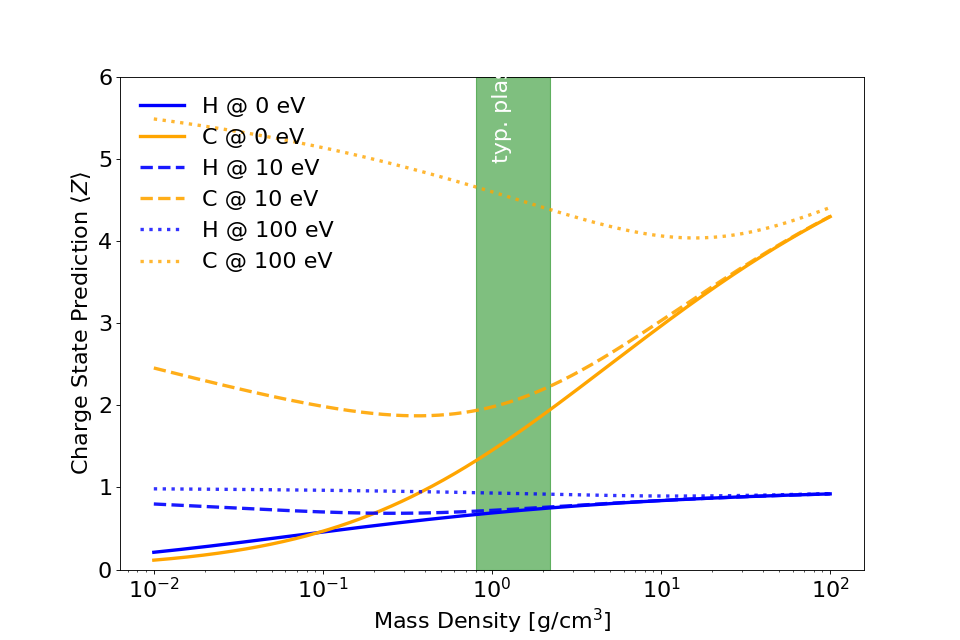
../_images/collisional_ionization_thomas-fermi_cutoffs.png
Two artifacts can be seen in this plot:

  1. Carbon is predicted to have an initial charge state \(\langle Z \rangle > 0\) even at \(T = 0\,\mathrm{eV}\).

  2. Carbon is predicted to have a charge state of \(\langle Z \rangle \approx 2\) at solid plastic density and electron temperature of \(T = 10\,\mathrm{eV}\) which increases even as the density decreases. The average electron kinetic energy at such a temperature is 6.67 eV which is less than the 24.4 eV of binding energy for that state. The increase in charge state with decreasing density would lead to very high charge states in the pre-plasmas that we model.

Implemented Cutoffs

To exclude regions of unphysical behaviour we have implemented the following cutoffs:

  1. Super-thermal electron cutoff

    We calculate the temperature according to \(T_\mathrm{e} = \frac{2}{3} E_\mathrm{kin, e}\) in units of electron volts. We thereby assume an ideal electron gas. Via the variable CUTOFF_MAX_ENERGY_KEV in ionizer.param the user can exclude electrons with kinetic energy above this value from average energy calculation. That is motivated by a lower interaction cross section of particles with high relative velocities.

  2. Lower ion-density cutoff

    The Thomas-Fermi model displays unphysical behaviour for low ion densities in that it predicts an increasing charge state for decreasing ion densities. This occurs already for electron temperatures of 10 eV and the effect increases as the temperature increases. For instance in pre-plasmas of solid density targets the charge state would be overestimated where

    • on average electron energies are not large enough for collisional ionization of a respective charge state

    • ion density is not large enough for potential depression

    • electron-ion interaction cross sections are small due to small ion density

    It is strongly suggested to do approximations for every setup or material first. To that end, a parameter scan with [FLYCHK2005] can help in choosing a reasonable value.

  3. Lower electron-temperature cutoff

    Depending on the material the Thomas-Fermi prediction for the average charge state can be unphysically high. For some materials it predicts non-zero charge states at 0 temperature. That can be a reasonable approximation for metals and their electrons in the conduction band. Yet this cannot be generalized for all materials and therefore a cutoff should be explicitly defined.

Non-Local Thermal-Equilibirium models

currently still in development

[More1985]

R. M. More. Pressure Ionization, Resonances, and the Continuity of Bound and Free States, Advances in Atomic, Molecular and Optical Physics Vol. 21 C, 305-356 (1985), https://dx.doi.org/10.1016/S0065-2199(08)60145-1

[FLYCHK2005]

FLYCHK: Generalized population kinetics and spectral model for rapid spectroscopic analysis for all elements, H.-K. Chung, M.H. Chen, W.L. Morgan, Yu. Ralchenko, and R.W. Lee, High Energy Density Physics v.1, p.3 (2005) http://nlte.nist.gov/FLY/